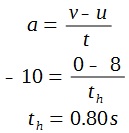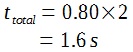Question

A student flips a coin into the air. Its initial velocity is 8.0 ms^-1. Taking g = 10 ms^-2 and ignoring air resistance, calculate:

a) the maximum height, h, the coin reaches, [2]
b) the velocity of the coin on returning to his hand, [1]
c) the time that the coin is in the air. [2]

Answer

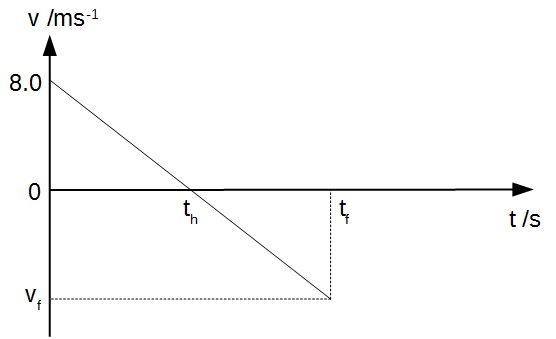
a) To easily solve the problem, the velocity-time graph has to sketched.

Since there is no air resistance, the acceleration will be constant at 10ms^-2 downwards. This means that the graph is a straight line.

At the highest point, the velocity of the coin will be zero.

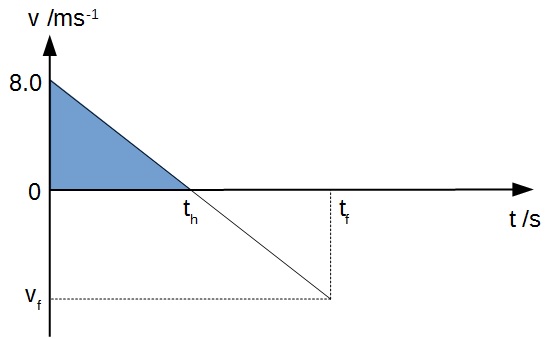
The maximum height is given by the shaded area below.

To find the area we first need to find the value of th. Since we are taking upwards to be positive, the acceleration is -10 ms^-2.

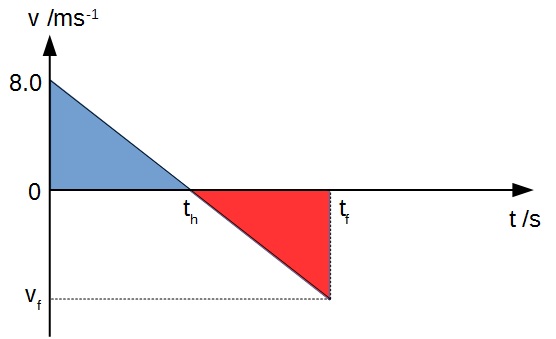
b) Since the coin falls back down to the student, the distance travelled downwards must be equal to the distance travelled upwards.

This means that the two shaded areas must be the same.

By symmetry, the final velocity of the coin must be -8.0 ms^-1.

c) Since the area of the shaded areas are the same, the time taken for the upward journey and the downward journey must also be the same.

Hence the total time taken is twice the time taken for the coin to reach the highest point.