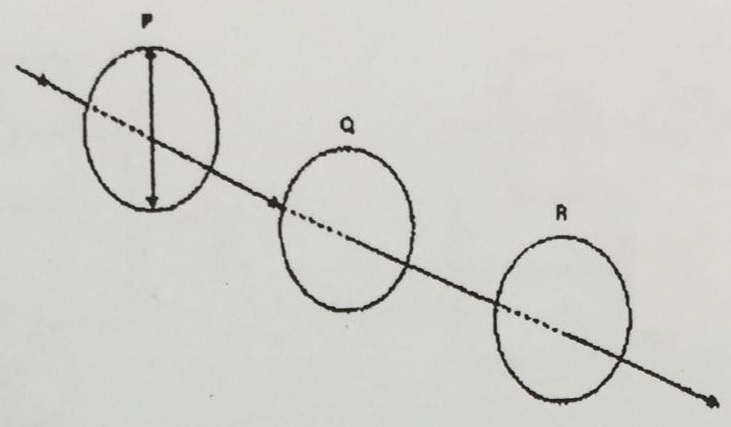
Question

A beam of initially unpolarised light passes through three polaroids P, Q and R. Polaroid P's axis of polarisation is vertical. Which orientation of polaroids Q and R with respect to the vertical axis will produce an emergent beam from polaroid R with maximum intensity.

Orientation with respect
to the vertical axis

         Q         R
A 45^o    45^o
B 45^o 90^o
C 90^o 180^o
D 180^o     60^o

Answer

When a wave polarised in one axis passes through another polaroid with the axis at an angle of θ, only the component of the wave parallel to the new axis can pass through.

A₁ = A₀ cos θ

After passing through the second polaroid placed at an angle of ϕ, the final amplitude will be given by

A₂ = A₁ cos ϕ

Hence, the final intensity will be given by

A₂ = A₁ cos ϕ
= ( A₀ cos θ ) cos ϕ

I₂ = k ( A ₂ )²
= k ( A₀ cos θ cos ϕ )²
= k A₀² cos² θ cos² ϕ
= I₀ cos² θ cos² ϕ

For option A,
I₂ = I₀ cos² θ cos² ϕ
= I ₀ cos² 45 ^o cos² (45^o - 45 ^o)
= 0.50 I₀

For option B,
I₂ = I ₀ cos² θ cos² ϕ
= I₀ cos² 45^o cos² (90^o - 45^o)
= 0.25 I₀

For option C,
I₂ = I₀ cos² θ cos² ϕ
= I₀ cos ² 90^o cos² (180^o - 90^o)
= 0

For option D,
I₂ = I₀ cos² θ cos²ϕ
= I₀ cos²180^o cos²(180^o - 60^o)
= 0.25 I₀

Hence, Option A will produce a beam with maximum intensity.