Question
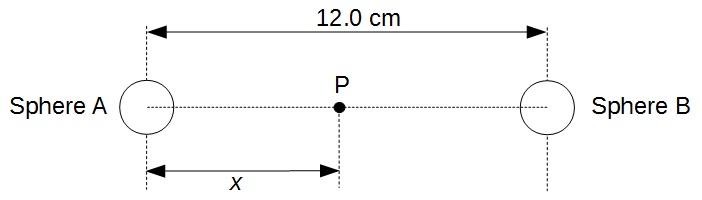
Two charged sole metal spheres A and B are situated in a vacuum. Their centres separated by a distance of 12.0 cm as illustrated in Fig. 2.1. The diagram is not to scale.
Point P is a point on the line joining the centres of the two spheres. Point P is a distance x from the centre of sphere A.
The variation with distance X of the electric field strength E at point P is shown in Fig 2.2. A positive value of E on the graph at a point corresponds to an electric field vector pointing horizontally to the right.
State and explain:
1. the signs of charges of A and B.
2. the ratio of the radius of sphere A to that of sphere B.
3. how the electric potential varies inside spheres A and B.
Answer
1. Both A and B are positive.
Near A, the electric field strength is positive. This means that the electric field strength is in the direction towards the right and away from A. This means that a positive point test charge will experience a force away from A. Hence A is positive.
Near B, the electric field strength negative. This means that the electric field strength is in the direction towards the left and away from B. This means that a positive point test charge will experience a force away from B. Hence B is positive.
2. From the graph, we can see that the radius of A given by the region from x = 0.0 cm to x = 1.4 cm where the electric field strength is zero. Hence, the radius of sphere A is 1.4 cm.
The radius of sphere B is given by the the region from x = 11.4 cm to x = 12.0 cm where the electric field strength is zero. Hence, the radius of sphere B is 0.6 cm.
Therefore, the ratio is 7 : 3.
3. The electric potential remains constant inside sphere A and sphere B. This is because the of the relationship \(E = -{dV \over dx}\). Since E is 0 inside the spheres, V must be constant in order for \( {{dV} \over {dx}} \) to be 0.
(Since the spheres are conductors, the electric charges in the form of mobile electrons inside are free to move. If there is a potential difference, there will be an electric force on the electrons. These electrons will move and redistribute themselves until there is a constant electric potential inside the sphere and no longer any electric force on the electrons.)