Question
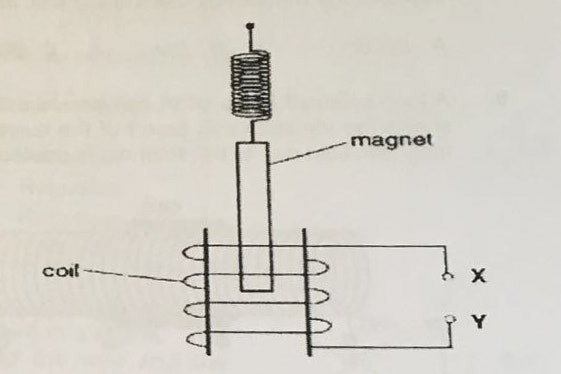
12) A long bar magnet is suspended from a helical spring so that one pole of the magnet lies within a long cylindrical coil as shown.
The magnet is given a small vertical displacement so that one pole of the magnet oscillates within the coil.
a) An induced e.m.f. is measured across the terminals of the coil.
i) Sketch the graph of e.m.f. against time to show how the induced e.m.f. varies with time for two periods of oscillation. [2]
ii) Using the principles of EM induction, explain the variation of the induced e.m.f. shown in your graph. [3]
b) State and explain a change that occurs in the amplitude of the oscillations of the magnet when a resistor is connected across XY. [3]
Answer
a) i) Assuming that the magnet is displacement upwards and then released, the induced e.m.f. is as shown:
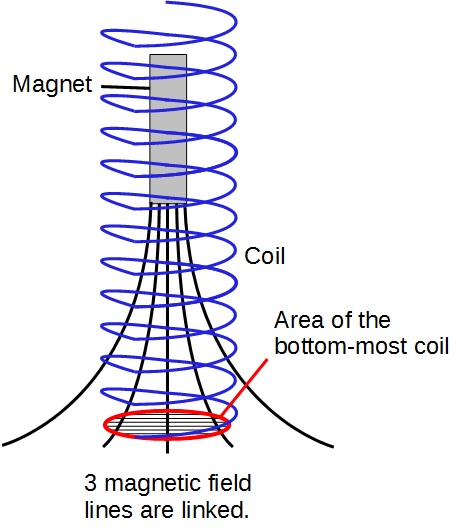
a) ii) At the top-most position, the magnetic flux linkage is the least. This because the magnetic field lines of the bar magnet spread out so the fewer magnetic field lines pass through the bottom-most coil.
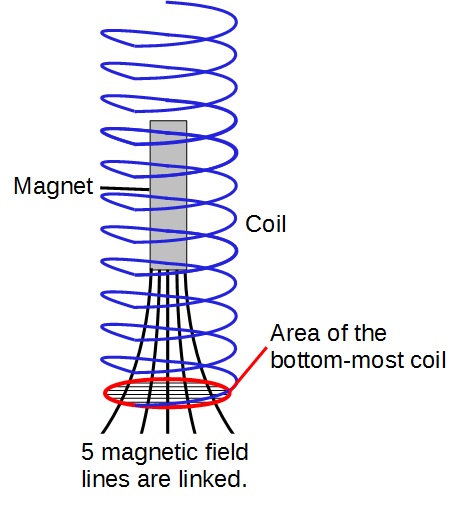
At the bottom-most position, the magnetic flux linkage is the greatest as most of the magnetic field lines pass through the bottom-most coil.
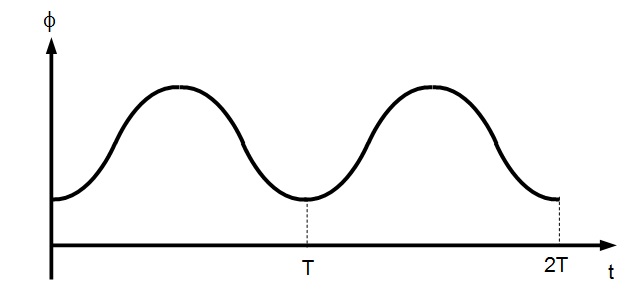
Assuming that the magnet is displaced upwards and released, the magnetic flux linkage varies as shown:
By using the relationship \( \varepsilon = -{{d \phi } \over {d t}}\) , the graph of the induced e.m.f. against time is obtained.
b) When a resistor is connected across XY, the induced e.m.f. will cause an induced current to flow.
According to Lenz's law, the induced current flowing in the coil will produce a magnetic field to oppose the change producing it. In this case, the magnetic field produced by the induced current will repel the magnet as it falls into the coil and attract the magnet as it rises away from the coil.
This causes the amplitude of the oscillation of magnetic to decrease with time. The kinetic energy of the magnet is converted into electrical energy which is then dissipated as thermal energy by the resistor.