Answers to questions posted by students
A big and warm thank you to the graduating students of 2019!
It has been a very rewarding experience tutoring all of you in preparation for the exams.
Hope you managed to catch the solar eclipse at at the end of Dec! (Scroll down for pictures.)
Wishing you the best for your results!
Portia, 26 Dec 2019
Erin, 26 Dec 2019
A circuit consists of three resistors, R1, R2 and R3, and two switches A and B, as shown in the figure.
The resistances between terminals X and Y is measured for different settings of the switches A and B. The results are shown in the table.
a) Determine the resistance of resistors R1, R2 and R3.
b) Switch A is now closed and switch B is open. Calculate the resistance between terminals X and Z.
a) From the first row in the table, when switches A and B are both open, the total resistance is 12Ω.
Assuming that X is positive and Y is negative, current will flow through the circuit as shown.
Hence, we see that:
From the second row in the table, when switch A is open and B is closed, the total resistance is 10Ω.
Assuming that X is positive and Y is negative, current will flow through the circuit as shown.
Hence, we see that:
From the third row in the table, when switch A is closed and B is open, the total resistance is 6Ω.
Assuming that X is positive and Y is negative, current will flow through the circuit as shown.
Hence, we see that:
Solving the equations:
we obtain
R2 = 4 Ω
R3 = 2 Ω
b) When switch A is closed and B is open, we need to find the total resistance between X and Z.
Assuming that X is positive and Z is negative, current will flow through the circuit as shown.
A man stands between two walls. He clapped his hands once and hears two echoes – one after 0.500 s and the other 0.300 s after the first. If the speed of sound in air is 330 ms-1, what is the distance between the two walls?
The first echo comes from the sound that travels to the nearer wall and reflects back.
The distance travelled by the sound is
Since the sound travels twice the distance between the man and the nearer wall,
The second echo comes from the sound that travels to the farther wall and reflects back.
We can calculate the distance travelled by the sound and the distance between the man and the farther wall.
Hence, the distance between the two walls can be found.
A molten alloy is made by mixing 450 g of molten cobalt of density 9.00 g/cm3 with 240 g of molten iron of density 8.00 g/cm3.
a) Calculate the density of the molten alloy in kg/m3. (An important assumption must be made to do this question.)
b) What is the assumption made in your calculation?
c)Suppose now a 150 cm3 molten alloy of cobalt and iron has a density of 8.74 g/cm3, calculate the volume of cobalt and iron in the alloy in cm3. (You may make the same assumption as in previous parts of the question.)
a) To find the density of the molten alloy, we need to find the total mass and total volume of the alloy.
We assume that the two metals do not react and that the total mass is the sum of their individual masses and the total volume is the sum of their individual volumes.
b) We assume that the two metals do not react and that the total mass is the sum of their individual masses and the total volume is the sum of their individual volumes.
c) To find the volumes of iron and cobalt, we first need to find the mass of the molten alloy.
We can then write down the relationships between the total mass and the mass of the cobalt and iron.
Similarly we can write down an expression for the volume of cobalt and iron.
Since we know the density of iron and cobalt, we can use the density to link the masses to their respective volumes.
Hence, the equation relating the total mass becomes:
We can now solve the following simultaneous equations:
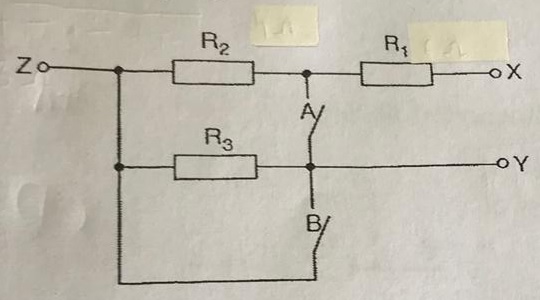
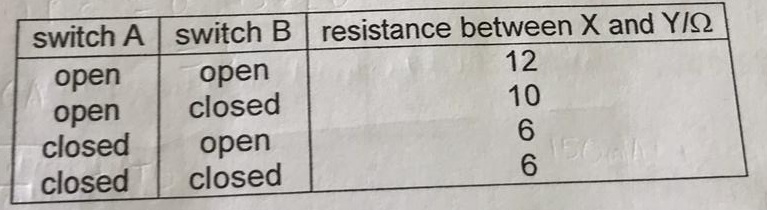
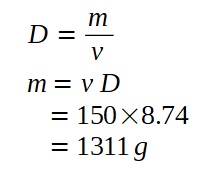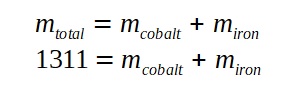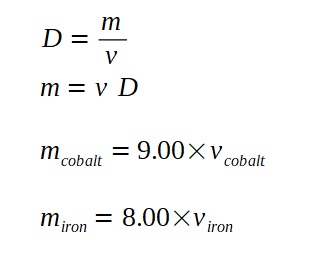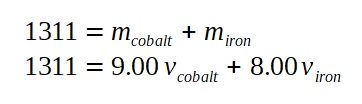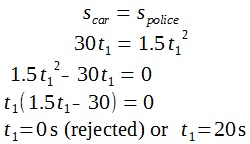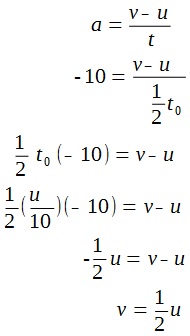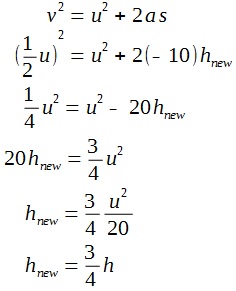A lamp is placed 30 cm above a metal surface which contains atoms of diameter 20 x 10-10 m. The lamp can be considered as a point source with power 0.015 W. It may be assumed that each electron can collect energy from a circular area which has a radius equal to that of the atom
a i) Find the intensity of the electromagnetic radiation directed on the atom.
ii) Hence, calculate the power incident on each atom.
iii) Determine, on the basis of wave theory, the time required for an electron to collect sufficient energy to be emitted from the metal if the work function of the metal is 3.2 x 10-19 J
iv) Comment on this calculation with actual experimental data and conclude the validity of wave theory.
a i) If we treat the lamp as a point source that emits light in all directions (3D),
Note that the area used is the total area which the power of the lamp is spread over.
aii) Now that we know the intensity of the light incident on the atom, we can calculate the power incident on the atom.
Note that the area used is the area of the atom which absorbs the power.
a iii) Since the electron requires a certain amount of energy to be emitted, we can calculate the time needed.
a iv) This calculation shows that if light were to be treated as a wave, the electron will required 7.68s to collect enough energy to be emitted. However, the experimental data shows that electrons will be emitted almost immediately, with a time much less than 7.68s.
This means that the wave theory cannot be used to describe the photoelectric effect.
A breathing monitor consists of an 8-turn coil attached to a patient’s chest. As a breath is inhaled, the area of the coil varies from 0.120 m2 to 0.124 m2. The magnetic flux density of the Earth is 50 x 10-6 T and makes an angle of 22.5o with the axis of the coil.
If the patient inhales for 1.59s, what is the average emf induced in the coil during the inhalation?
A) 0.116 μV
B) 0.126 μV
C) 0.930 μV
D) 1.01 μV
To calculate the induced emf, the magnetic flux linkage of the coil has to be calculated.
Before inhalation,
After inhalation,
The induced emf can now be calculated.
Answer is C
A displacement against position graph for a longitudinal wave is shown below. Which points represents the compressions and rarefactions?
For the graph, the position axis represents the location of the equilibrium position of a particle. The displacement axis gives the displacement of the particle from its equilibrium position. For this question, we assume that positive displacement is towards the right.
For example, in the graph below, Particle A has a equilibrium position at 0.80 m and it is displaced 1.5 mm to the right of its equilibrium position.
We can show the displacement on the graph:
The displacements of B1, B2, B3, C1, C2 and C3 are shown.
Hence, B2 is the compression and C2 is the rarefaction.
Two resistors R1 and R2 are connected up in a circuit as shown in the figure below.
When the switch S is open, the ammeter reads 1.0 A and the voltmeter reads 8.0 V.
When the switch S is closed, the ammeter reads 1.5 A and the voltmeter reads 6.0 V.
Determine the values of R1 and R2. Show your working clearly.
When the switch S is open, the current only flows through R2.
The circuit can be simplified as shown:
We can calculate the value of R2 directly.
When the switch S is closed, the current flows through both R1 and R2.
We can calculate the resistance across XY:
Since R1 and R2 are connected in parallel and we know the resistance across XY,
Hence, R1 is 8.0 Ω and R2 is 8.0 Ω
In two widely-separated planetary systems whose suns have masses S1 and S2, planet P1 of mass M1 and planet P2 of mass M2 are observed to have circular orbits of equal radii respectively. If P1 completes and orbit in half the time by P2, it may be deduced that
A) S1 = S2 and M1 = 0.25 M2
B) S1 = 4 S2 only
C) S1 = 4 S2 and M1 = M2
D) S1 = 0.25 S2 only
E) S1 = 0.25 S2 and M1 = M2
For the system with S1 and P1, the gravitational force on P1 provides the centripetal force.
Similarly for the system with S2 and P2,
Since the period of P1 is half of P1,
Since the periods do not depend on the masses of the planets, we can only deduce that S1 = 4 S2.
Hence, answer is B.
At a point outside the Earth and a distance of x from its centre, the Earth’s gravitational field strength is 5 N kg-1. At the Earth’s surface, the field strength is about 10 N kg-1. Which of the following gives an approximate value for the radius of the Earth?
A) x/5
B) x/2√2
C) x√2
D) x/√2
At point x, the gravitational field strength is given by the formula:
At the surface of the Earth, the gravitational field strength is given by the formula:
Since gs ≈ 2 gx,
Hence, the answer is D.
A wire that obeys Hooke’s Law of length x1 when it is in equilibrium under tension T1. It’s length becomes x2 when the tension is increased to T2. What is the extra energy stored in the wire as a result of this process?
A) 1/4 ( T2 + T1 ) ( x2 - x1 )
B) 1/4 ( T2 + T1 ) ( x2 + x1 )
C) 1/2 ( T2 + T1 ) ( x2 - x1 )
D) 1/2 ( T2 + T1 ) ( x2 + x1 )
E) ( T2 - T1 ) ( x2 - x1 )
The extra energy is stored as elastic potential energy.
The graph of tension against total length is shown below. The extra elastic potential energy is given by the shaded area.
Answer is C.
All the Best to Graduating Students of 2017
A heartfelt thank you graduating students of 2017!
It has been a very memorable journey tutoring all of you in preparation for your exams this year.
The examinations have been difficult and you deserve a well-needed rest!
Wishing you the best for your results!
O-Level results will be released from mid January 2018 onwards.
A-Level results will be released from early March 2018 onwards.
Daniel, GCE O Level
Gunjita, GCE A Levels
Galbraith GCE O Level
Haley, GCE O Levels
Joshua, GCE O Levels
Matthew, iGCSE
Malcolm, GCE O Levels
Shao Xian, GCE A Levels
Tze Han, GCE O Levels
Brendan, GCE A Levels
A metal nugget floats in between some water and mercury. The densities of the metal nugget, mercury and water are 7900 kg m-3, 13600 kg m-3 and 1000 kg m-3 respectively.
What is the ratio of the volume of the nugget submerged in water to that of mercury?
A) 0.541
B) 0.826
C) 0.924
D) 1.21
Since the nugget is suspended in the liquids, the weight of the nugget is equal to the upthrust.
The nugget displaces both water and mercury, hence, the upthrust is due to the both the weight of the water displaced and the weight of the mercury displaced.
The volume of the nugget is the sum of the volume of water displaced and the volume of mercury displaced.
The answer is B.
Two containers of volume 4.0m3 and 6.0m3 contain an ideal gas at pressures of 100Pa and 50Pa respectively. Their temperatures are equal. They are joined by a tube of negligible volume. The gas flows from one container to the other with no change in temperature. The final pressure will be
A) 70 Pa
B) 75 Pa
C) 80 Pa
D) 150 Pa
Before the valve is opened, we first find an expression for the initial number of moles of gas in each container:
Now, the total initial number of moles of gas can be found:
After the valve is opened, the pressure in each container is now the same and the temperature remains the same.
The new expression for the final number of moles in each container is found again:
Now, the total final number of moles of gas can be found:
Since the total number of moles remains the same,
Answer is A.
A light ray travels from a Perspex block into the air.
The critical angle of Perspex is 42.9o
What is the angle of refraction when the angle of incidence is 36.0o?
A) 23.6o
B) 24.5o
C) 52.9o
D) 59.7o
In order to calculate the angle of refraction, the refractive index of Perspex has to be found first.
Using the critical angle,
Now that the refractive index of Perspex is known, the angle of refraction can be calculated.
The answer is D.
The diagram shows an object O viewed using 2 mirrors.
A person looks into the mirror as shown.
At which position is the image of O seen?
The object O is first reflected in top mirror to form the first image.
(Object distance is equal to Image distance)
The first image is then reflected in the bottom mirror to obtain the final image.
(Object distance is equal to Image distance)
Answer is D.
A copper bar of length L is moving to the right with a uniform speed v in a region of uniform magnetic field of flux density B, directly perpendicularly downwards into the paper in the figure below.
The ends of the rods are rigidly connected to a voltmeter which moves with the rod. What is the reading on the voltmeter?
A) zero
B) non-zero reading less than Blv
C) BLv
D) more than BLv
Method 1:
Consider wires PQ and RS. Since both wires are moving through the magnetic field, both of them will have an induced e.m.f. of BLv.
Based on Fleming’s Right Hand rule, the induced current of PQ and RS will both be upwards.
This means that the resultant current will be zero and the e.m.f. measured by the voltmeter will be zero.
Answer is A.
Method 2:
Consider the closed loop PQRS. As the loop moves through the magnetic field, the magnetic flux linkage remains the same since the area of the loop does not change.
Since there is no change in the magnetic flux linkage, by Faraday’s law there is no induced e.m.f. and the voltmeter will read 0 V.
Answer is A.
An e.m.f. is induced in a coil placed in a changing magnetic field. The flux density B of this field varies with time as shown below.
At which value of t is the magnitude of the e.m.f. induced in the wire a maximum?
A) 1 ms
B) 2 ms
C) 3 ms
D) 4 ms
The induced e.m.f. is given by the formula:
Hence the magnitude of the induced e.m.f. is given by:
This means that the induced e.m.f. will be the greatest when the rate of change of the magnetic flux density is the greatest.
From the graph, the rate of change of the magnetic flux density is the greatest when the gradient of the graph is the greatest.
This means that the induced e.m.f. will be the greatest at time t = 0 ms and t = 4 ms.
Hence the answer is D.
A car travelling at a constant speed of 30 ms-1 passes a police car, which is at rest.
The police officer accelerates at a constant rate of 3.0 ms-2 and maintains this rate of acceleration until he pulls next to the speeding car. Assume that the police car starts to move at the moment the car moves past the police car.
What is the time required for the police officer to catch up with the car?
We assume that the police car catches up with the car at time t1.
The following formula for displacement can be obtained:
When the police car catches up with the car, both have travelled the same displacement.
The police car requires 20 s to catch up with the car.
A body is thrown vertically up from the ground with an initial speed u and it reaches the maximum height h at time t0.
What is the height it reaches at ½ t0?
We first define the upwards direction as positive.
When the body reaches the maximum height, the speed of the body is 0.
Knowing this, we can find expressions for h and t0. The acceleration of the body is taken to be 10 ms-2 downwards. Since we define upwards to be positive, the acceleleration will be -10 ms-2.
When the time is ½ t0,
Now that we know the speed at ½ t0, we can find the height travelled by the body.
